このセクションの他の記事
精度評価の見方（時系列解析）
＜予測値＞
AIが予測した値と実測値を時系列にグラフで表示します。
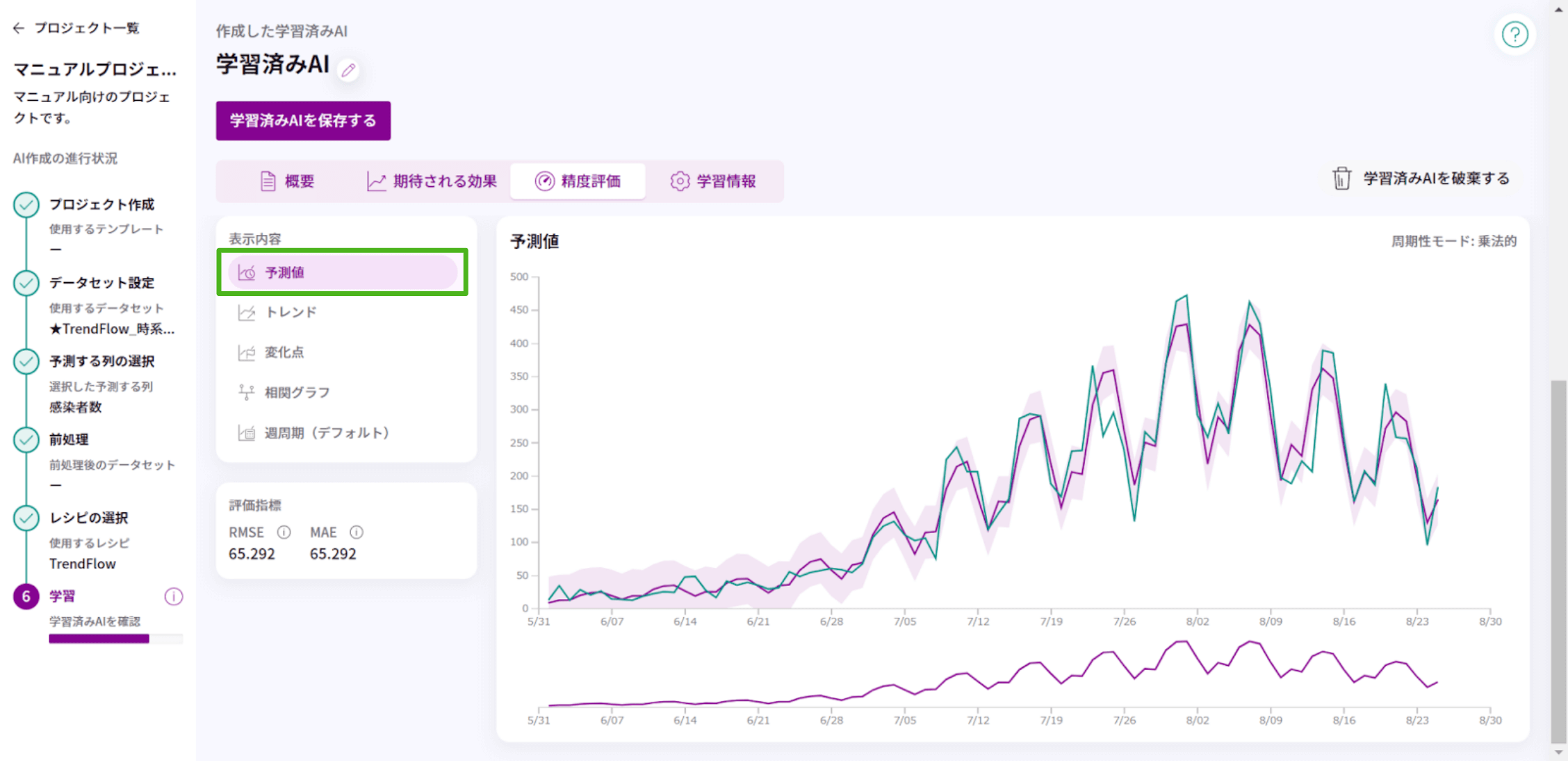
紫の線は予測値（AIが導き出した値）です。
緑の線は実測値（投入したデータの値）です。
マウスオーバーすると吹き出しで値が表示されます。
紫線と緑線が近いほど、学習に使用したデータセットにおいては精度よく予測ができていることを表します。
薄紫の帯は95%信頼区間です。95%信頼区間とは統計の用語で、予測値が95％の確率でこの範囲に含まれることを表します。
グラフ下の縮小図をドラック＆ドロップすると、その範囲のグラフを拡大表示します。
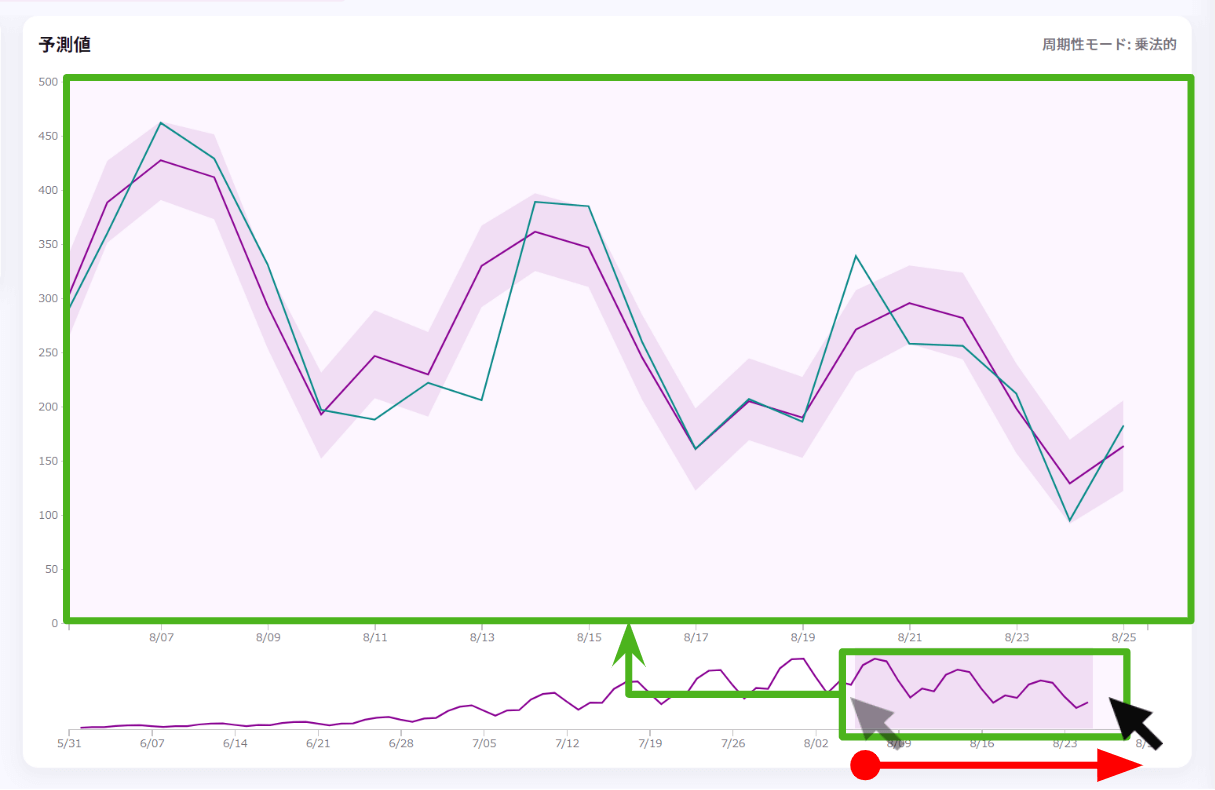
＜トレンド＞
時系列データの増減の傾向を確認できます。
時系列データには時間の経過とともに増加したり減少したりする動きが見られます。この変化のことをトレンドといいます。
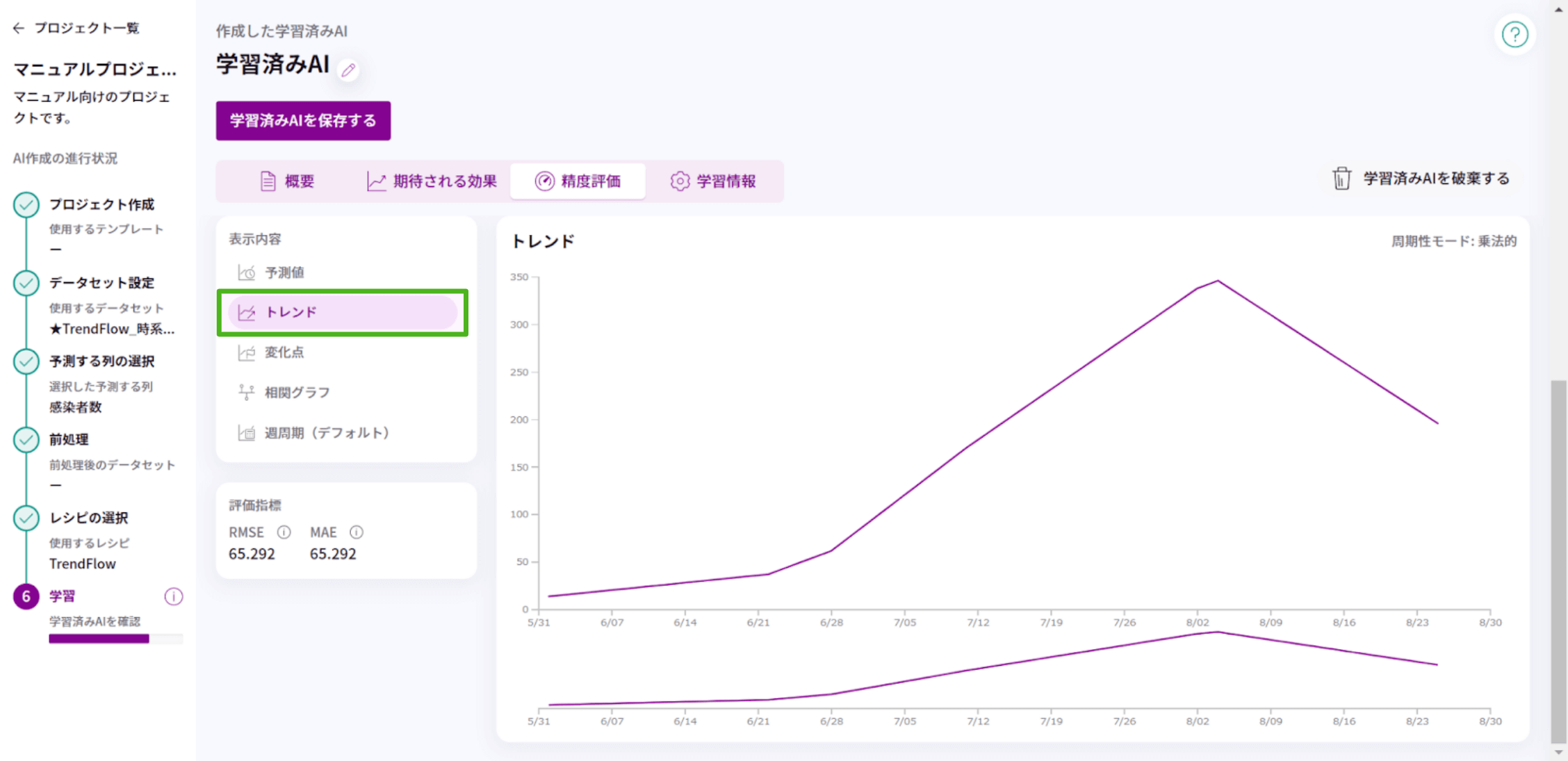
例えば上のトレンドグラフからは、6/28を境に顕著に増加し始め、8/4をピークに減少していくことが読み取れます。
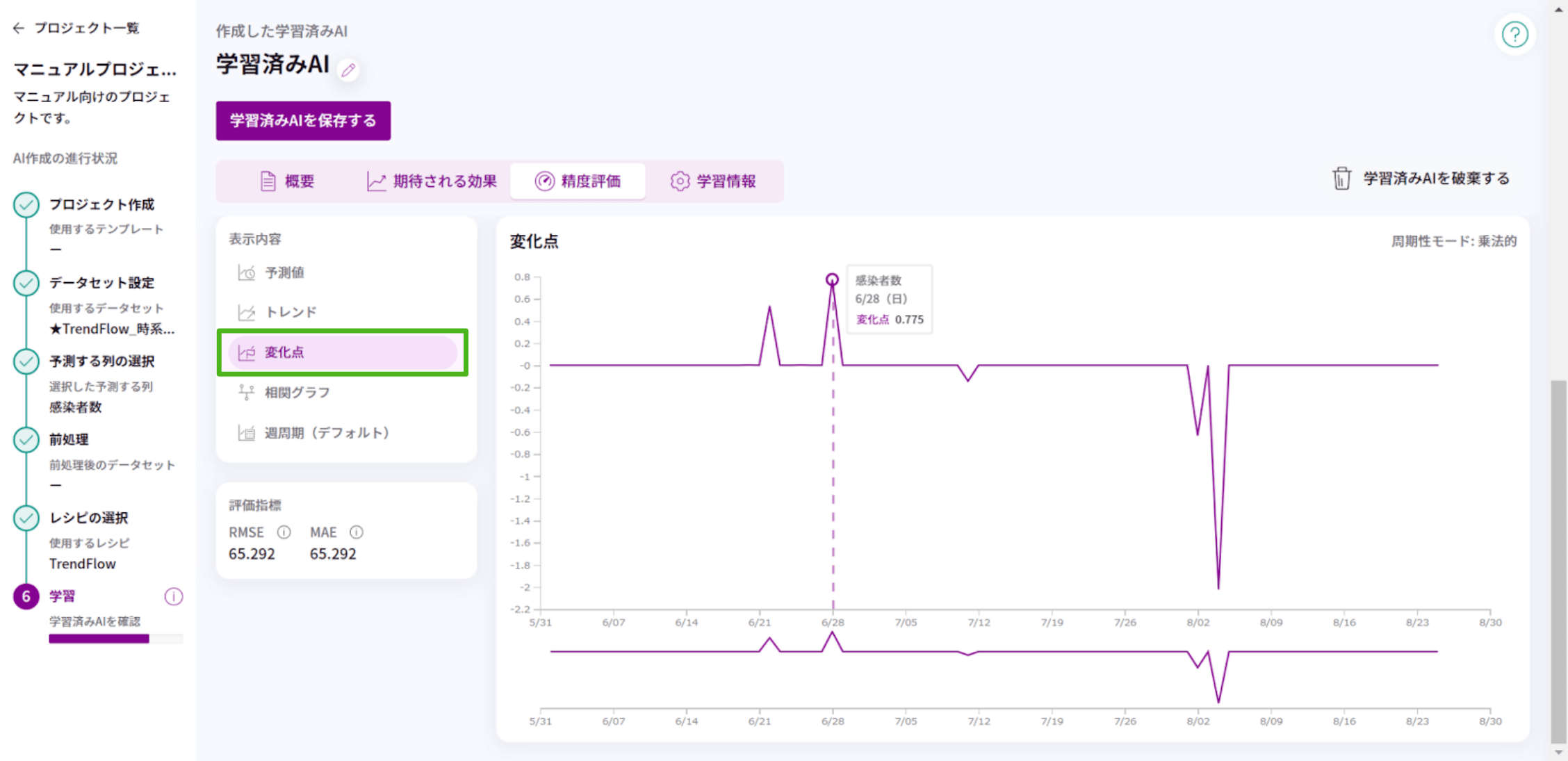
＜変化点＞
急激に値が変化した時点を可視化します。
異常を検知したい場合など、このグラフから異常が起こった日付や時間を特定することができます。
＜相関グラフ＞
「コレログラム」ともいい、2種類のデータの関連性の強さを可視化します。ここからデータの周期性を読み取ることができます。
データに欠損値がある場合は可視化することができません。その場合は、前処理でデータセットの欠損値を取り除いて下さい。
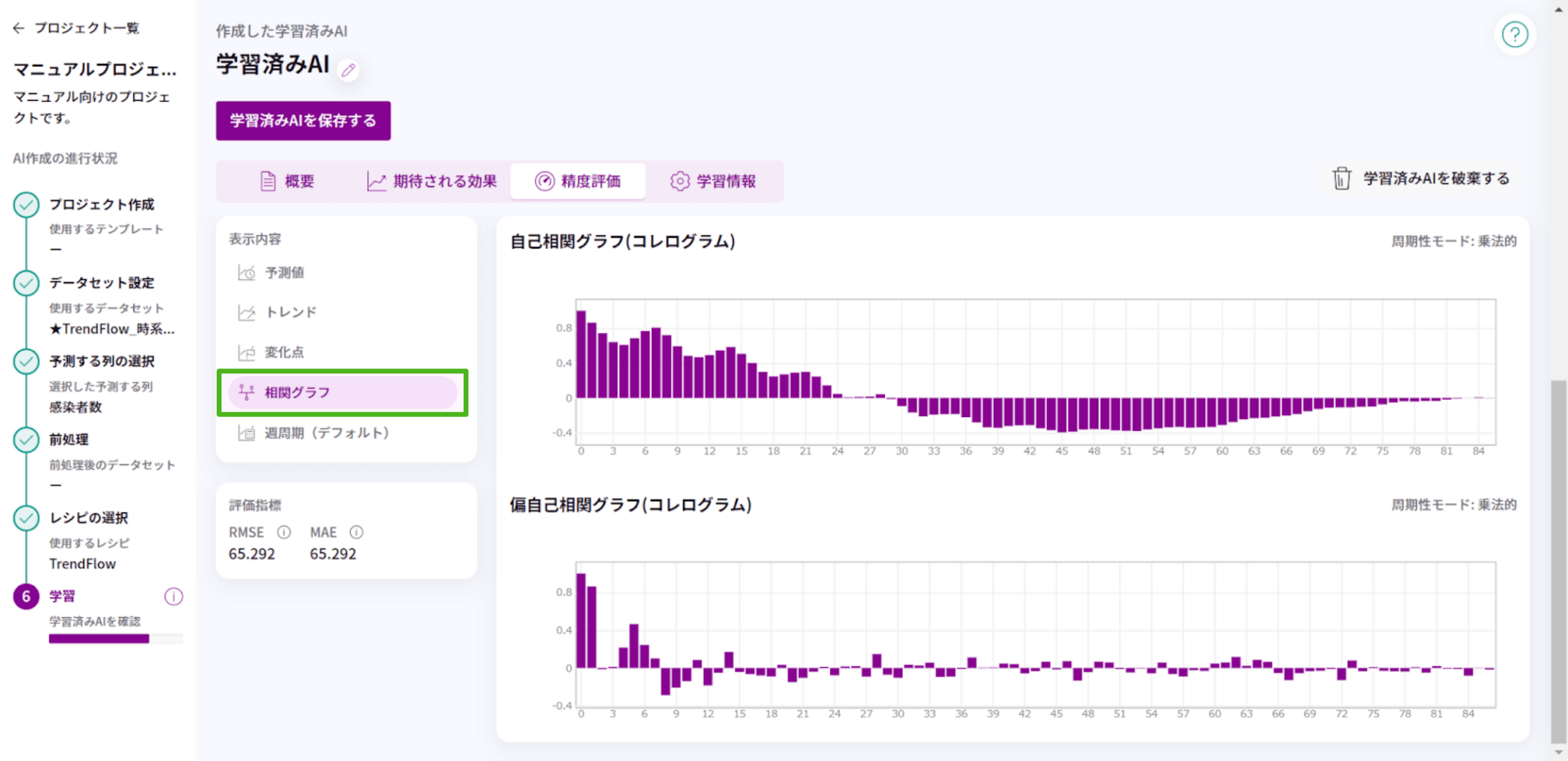
x軸：ラグ（元データからどのくらい時間をずらしているか 量や指標を表す）
y軸：相関係数（元データとずらしたデータの相関の強さを表す）
＜相関係数について＞
相関係数が1に近い：正の相関（片方が増加すればもう片方も増加する）
相関係数が-1に近い：負の相関（片方が減少すればもう片方も減少する）
相関係数が0に近い：相関がない ことを表します。
＜自己相関と偏自己相関について＞
自己相関は、元データからある一定の時間ずつずらしたデータ（1次遅れ、2次遅れ・・・n次遅れ）を作成し、元データとそれぞれの遅れデータとの相関関係を表します。
時間をずらしたデータは元データの時間をずらしただけですので、元データと同一のデータです。このような2つのデータの相関関係を自己相関といいます。
相関係数の絶対値が高いラグほど元データと似た変化をしていることを示すので、何次遅れのデータが元データと強い相関があるかを知ることができます。また、周期的に相関係数の絶対値が高いラグが現れる場合、そこに周期性があることを示します。
対して偏自己相関は、自己相関係数から、時間によって受ける途中の時間の影響を除いた相関関係を表します。
※ 統計学の範疇ですので本マニュアルでは詳しく解説しません。詳細はWebや書籍などをご覧ください。
＜周期＞
データの周期性を可視化します。
レシピを作成する際に、TrendFlowブロックの［自動周期設定］をonにするか、周期を手動で追加した場合にのみ表示されます。
自動周期設定はデフォルトonです。
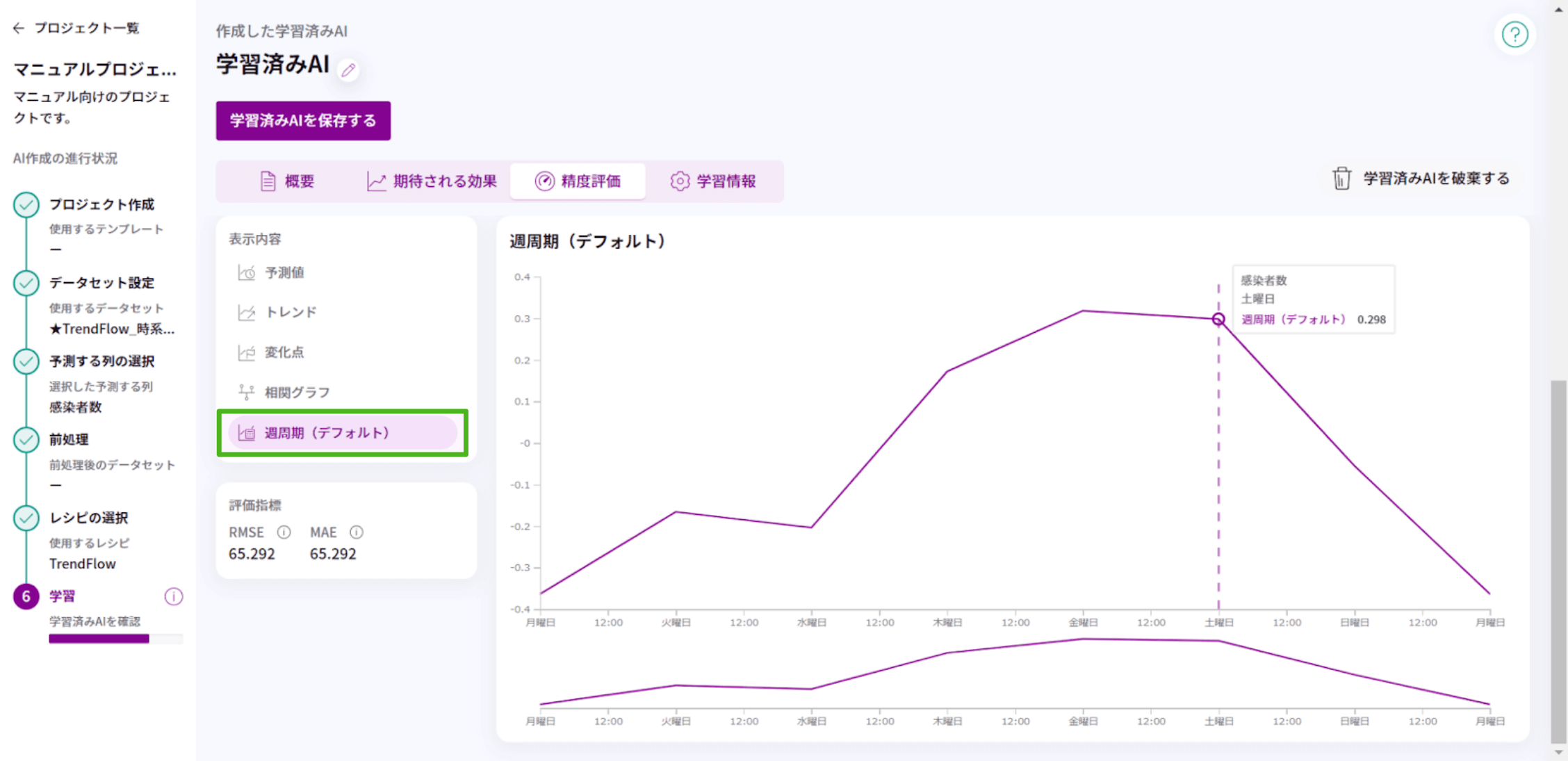
グラフの名前は、自動周期設定の場合、AIが自動で判断した「〇周期（デフォルト）」と表示し、手動で周期を追加した場合、追加したときに設定した「周期の名前」を表示します。
周期の設定方法については、TrendFlowとは をご覧ください。
＜評価指標＞
学習に使用していないテストデータを使って求めた、AIモデルの性能を評価する値です。
表示する指標は RMSE と MAE の2種類で、どちらも実測値と予測値の誤差を測る指標です。
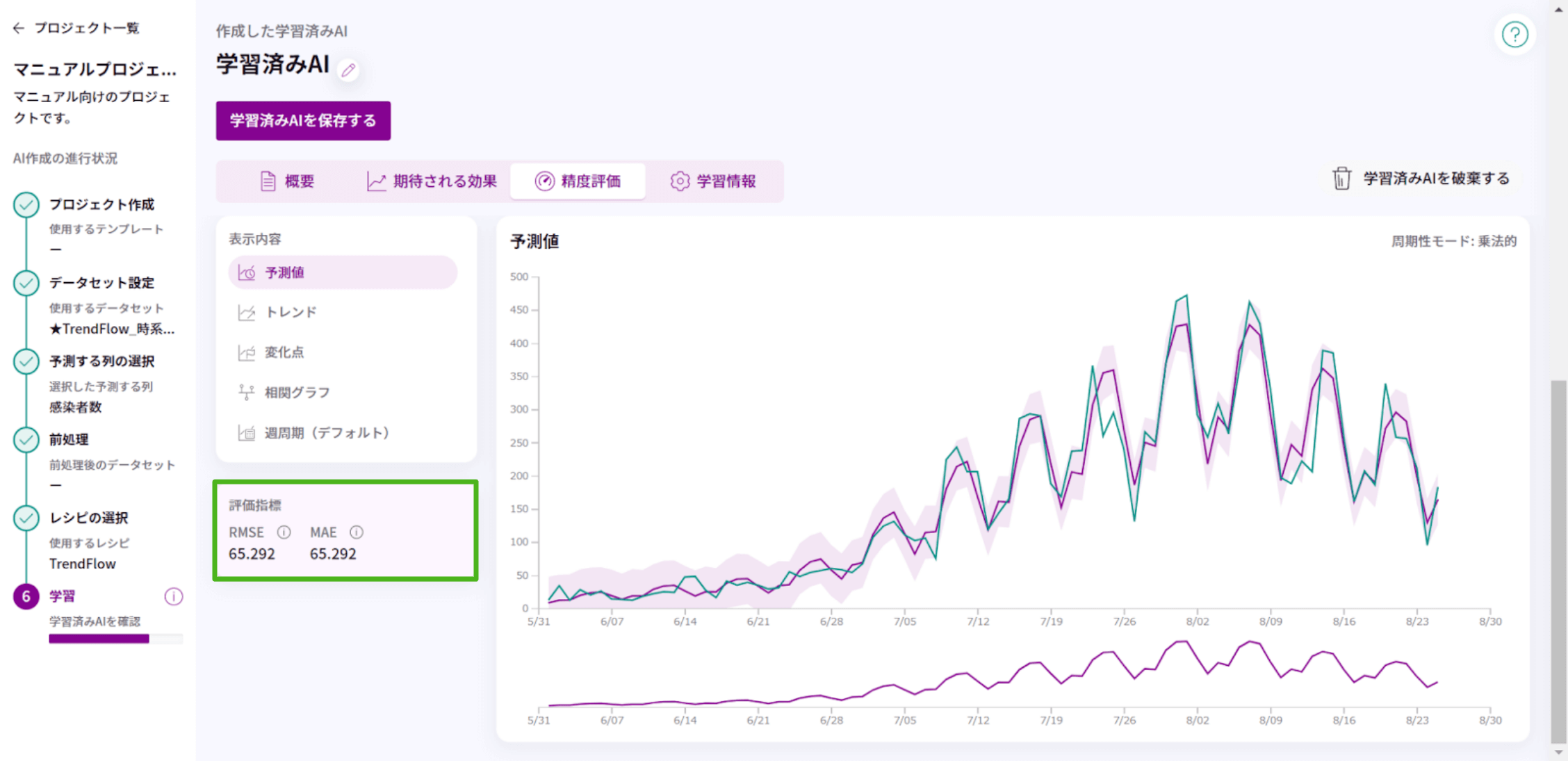
・RMSE (Root Mean Squared Error, 二乗平均平方根誤差)：
全データの実測値と予測値の「誤差の2乗の平均を求めて平方根を取った値」です。
実測値と予測値が近づくほど値が小さく、0に近いほど予測精度が良いことを表します。
・MAE (Mean Absolute Error, 平均絶対誤差)：
全データの実測値と予測値の「誤差の絶対値の平均」です。
実測値と予測値が近づくほど値が小さく、0に近いほど予測精度が良いことを表します。
誤差が一定の場合、RMSEとMAEの値に大きな差は出ません。しかし、RMSEは計算の際に実測値と予測値との誤差を2乗しているため、双方の値が離れるほど指数関数的に増えます。つまり、外れ値の影響を受けやすいということです。MAEは誤差を2乗していないため、外れ値の影響を受けにくいと言えます。
RMSEは、大きな予測誤差が生じてもよい場合（外れ値も考慮したい場合）に向いており、
MAEは、誤差を平均的に評価したい場合（外れ値を考慮したくない場合）に向いていると言えるでしょう。